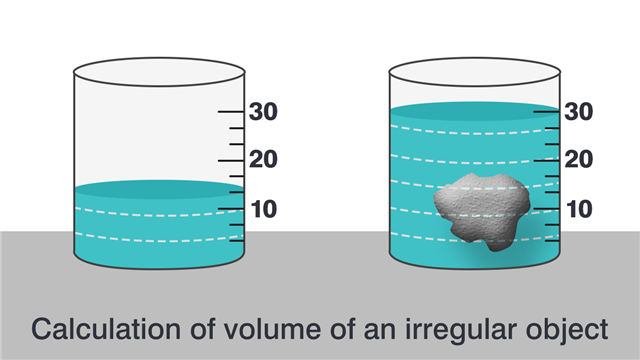
Science teaches us to think out of the box. So while others may only use water for drinking and bathing, we shall learn how to use it to find the volume of an object.
Even the Crow uses it!
Remember the old Aesop fable, The Crow and the Pitcher? In it, the crow is able to raise the water level by dropping stones in the pitcher. This actually is a very good practical application of the water displacement method.
Imagine a world made up of just cylinders, cones, cubes, and spheres. How easy it would be to apply mathematics in a regular and well-defined place such as that! For instance, all you would need to do is memorize a set of four formulas, and you would easily be able to find out the volume of just about anything. But before you request the creator to revise His design, ask yourself, would you really want to live in such a place?
The flowing curves and random edges of the different things around us, are precisely what make them so beautiful to look at. The world with all its irregularities is perfect just the way it is. And in order to live here, we don’t have to sacrifice mathematics either, thanks to one remarkable ancient Greek thinker and inventor, Archimedes.
Among Archimedes’s many wonderful inventions is what is known today as the water displacement method. It can be used to accurately calculate the volume of any object no matter what its shape, and the best part is that it doesn’t involve any complex mathematical calculation either. It is as simple as it is ingenious. In the following sections, we shall find out how it works. But before that, let’s first examine how the great Archimedes came up with this idea.
Story Behind the Invention
Archimedes lived in Syracuse, Greece over 2,000 years ago. He was a physicist, a mathematician, an engineer, and an astronomer. The tales of his wisdom and genius were well-known throughout the land.
The king of Syracuse had a golden crown made by one of the finest jewelers in his kingdom. The king himself had supplied pure gold required for it. The jeweler had done a fine job in making the crown, but the king suspected that he had adulterated the pure gold with silver. However, since there were no means of testing the purity of a metal at the time, the jeweler’s claim couldn’t be verified. The king summoned Archimedes and assigned him the task of verifying the authenticity of the golden crown, but without destroying it.
It was a real challenge! Archimedes worked for many days, tried every known method and applied all his mathematical knowledge; however, he just simply couldn’t come up with a solution. One day, while still struggling with the problem, Archimedes decided to take a soothing bath to clear his head. He had a bathtub filled with water and made ready for him.
As Archimedes stepped into the full bathtub, he noticed that some water in it, splashed out. When he submersed more of his body, even more water over-flowed. Right away, he knew that he had found the answer to the king’s problem.
So excited was he, that he hopped off the bathtub and ran through the streets stark naked shouting ‘Eureka, Eureka!!!’ He submitted his results to the king using which, the king was able to prove that indeed the jeweler had cheated him by adding silver to the crown.
Today Archimedes’s method is known as the water displacement method and is widely used for its simplicity and accuracy.
How Does the Method Work
So how was Archimedes able to verify the make of the crown by observing the overflow of water from his bathtub?
When Archimedes stepped into the bathtub and saw that the water in it overflowed, he immediately realized that there was some connection between the occurrence of the two events. When he immersed himself further and saw that more water overflowed, he knew at once that the relation between his mass and that of the overflowing water was a direct one.
He realized that if the crown is submersed completely and the exact amount of water that overflows as a result is measured, it would be equal to the volume of the crown. Once the volume is known, its density, which is its mass divided by its volume, could be calculated.
The density of the crown would be lower than that of pure gold if a cheaper and less dense metal such as silver was added to it. Thus it was a thorough test using which, Archimedes was able to prove the falsity of the jeweler.
The water displacement method, can be used to accurately find out the volume of an object of any shape. Basically, it relies on the fact that for all practical purposes, water is incompressible. So when an object enters water held in a container, the water gets displaced to make room for it. The object thus when fully submersed, displaces a volume of water which is exactly equal to its own volume.
Buoyancy: On being dropped in water, some objects tend to sink while others float. Archimedes understood the reason behind this and formulated a principle explaining it, known today as the Archimedes principle.
Archimedes Principle: Any object completely or partially immersed in a liquid, is buoyed up with a force which is equal to the weight of the fluid that the object displaces.
Thus, if an object displaces a larger weight of fluid, it will float, otherwise it will sink. Large ships, although being very heavy, are able to float as they displace several tons of water. A small stone on the other hand is much lighter in weight. However, it still sinks because it is able to displace only a small weight of water.
How to Find Volume
The Archimedes water displacement method is one of the most convenient and easiest methods of measuring the volume of an irregularly shaped object. And you don’t need a bathtub for it to work either! As you will see, you can practically apply this method with just a few basic equipment and by using the following steps.
Requirements:
- An irregular object.
- A graduated cylindrical measuring flask, big enough for the object to fit in.
- A notebook and a calculator.
Note: Measuring flask readings are in ml.
Procedure:
- Fill the measuring flask with an adequate amount of water. The basic idea here is not to fill it past its uppermost marking. A good way to ensure this is by only filling the flask halfway through, leaving enough markings above the water level.
- Once the water settles down, read the marking at bottom of the meniscus that is, the curved water-level line. This is the initial volume of water inside the measuring flask. Note it down as ‘Vol1’. In our example, the initial level of water is at 13.33 ml. Thus Vol1 = 13.33 ml.
- Now take the irregular object whose volume you wish to measure, and gently drop it into the flask. Allow some time for the water to settle, and note the marking corresponding to the risen water level. This is the volume of the water plus that of the object ‘Vol2’. In our example, Vol2 = 30 ml.
- Now use the following formula to calculate the volume of the object.
Volume(object) = Volume(water + object) – Volume(water)
Volume(object) = Vol2 – Vol1
Volume(object) = (30 – 13.33)
Volume(object) = 16.66 ml.
Once you have understood the steps shown above, try solving the examples to get a better understanding of the water displacement method for calculating volume.
Note: Measuring flask measurements are in ml.
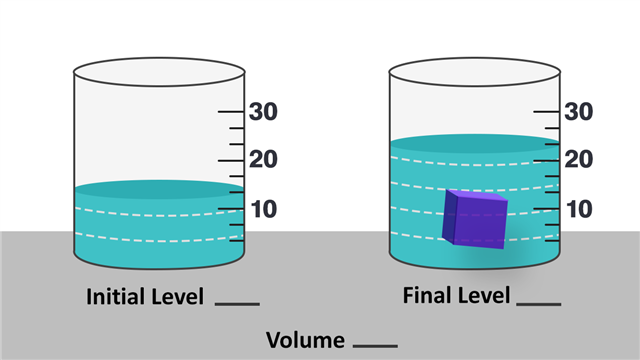
Example 1
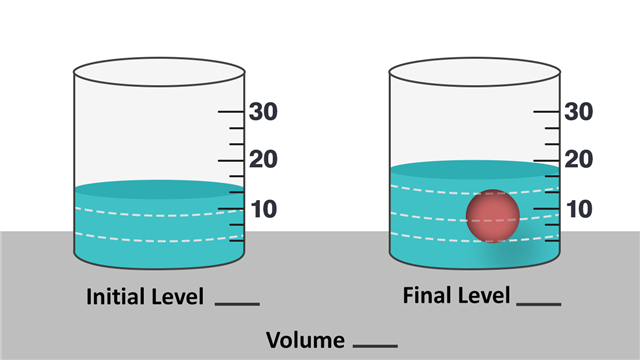
Example 2
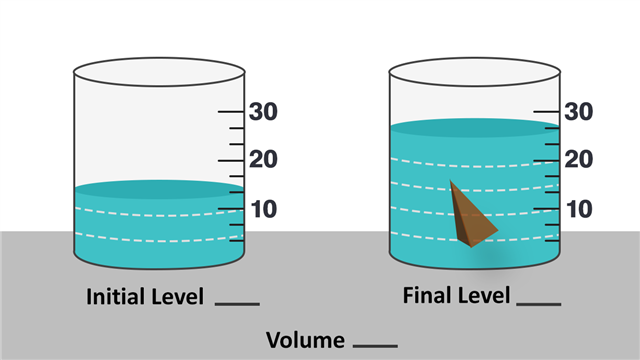
Example 3
How to Find Density
Archimedes was able to calculate the density of the crown using the water displacement method. We too can calculate the density of any irregular object by using the steps given below.
1) Find the volume of the object as described in the previous section.
2) Use a weighing machine to find the mass of the object. Now, from the definition of density, we arrive at the following equation which can be used to calculate the density of the object:
Density = Mass ÷ Volume
For example, if the calculated volume of object is 4 ml. and its mass is 8 gm, then its density will be (8 ÷ 4) = 2 gm/ml
Thus Archimedes, over 2,000 years ago, came up with the water displacement method which could be used to find the volume of an irregular object. The invention of this method was a great achievement back then, and it is still relevant in modern times, owing to its simplicity and high degree of accuracy.