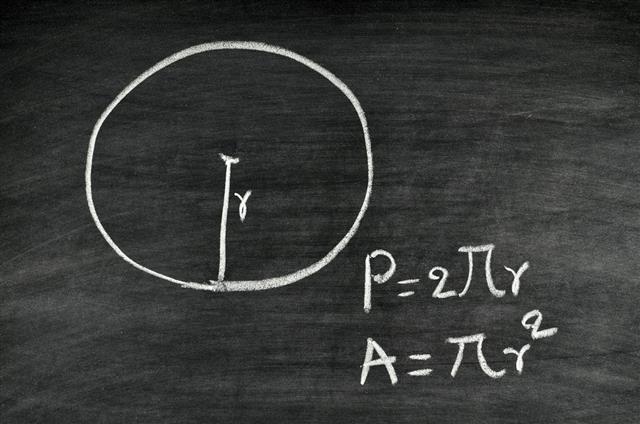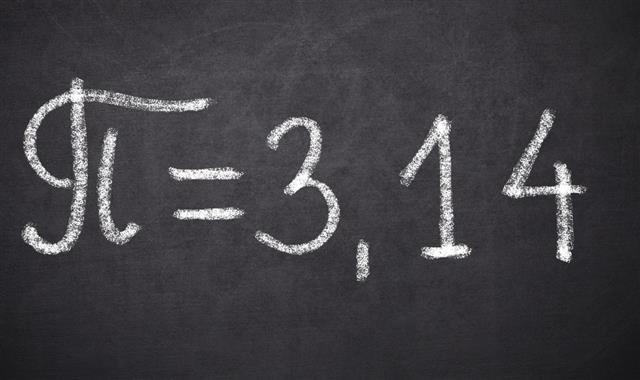In order to learn how to find the circumference of a circle, one needs to know the formula and plug in the values according to it.
Of the various two dimensional geometrical figures, the circle is one with no side or end. It is similar to a ring. Its circumference is what a perimeter is to a square or a rectangle.
In simple language, it is the rim of the ring. If we take a string and make a circle out of it, then the entire length of the string would give its circumference. Other than being able to solve problems given as homework, there are various practical applications for which we need to know how to find the circumference of a circle.
Different Parts of the Geometric figure
There is a formula, which can be used to calculate the circumference. However, before using the equation, one should be conversant of its various parts/aspects.
★ The Center: It is the exact point inside the figure, such that all points are equidistant from it. Each circle has just one center.
★ Radius (r): Radius is the shortest distance of the center from any point on the circle.
★ Diameter (d): It is a straight line that starts and ends in two points on the figure, and also passes through the center. Hence, as per this definition, the diameter is twice the radius. Alternatively, it could be explained as two radii placed end to end. (Formula for diameter is : d=2r)
★ Chord: One should be clear about the chord to avoid confusion with the diameter. Like a diameter, a chord is also a straight line that touches any two points of the circular figure, however, it does not pass though the center. Conversely, any chord passing through the center is the diameter.
★ Pi (π): Pronounced as pie but written pi, π is an irrational number. If written in the form of a decimal, it will never end. Hence, it is used in formulas, and is given the approximate value of 3.14.
Procedure
★ Step 1: The first step is to know the formula. There are two formulas that can be used for the purpose. They are:
- Formula 1: C = π x diameter
- Formula 2: C = π x 2 radius
★ Step 2: The next step is to obtain the values for the radius or diameter. Write them down on the paper on which you would be recording the value. Now, plug the values in the formula and calculate.
An Example
Using the Radius
If the value of the radius is known, then it can be put in the formula directly. For example:
Given that the radius is 3 cm, the circumference C = π x 2 radius,
or, C= 3.14 x 2 (3) cm,
or, C= 18.84 cm
Using the Diameter
If the value of the diameter is known it can be directly put in the equation. For example:
Given that the diameter is 6 cm, the circumference C= π x diameter,
or, C= 3.14 x 6 cm,
or, C= 18.84 cm
Importance
Knowing how to calculate this value is important, as there are quite a few practical applications for it. For example, what if you have a circular garden and you want to lay bricks all around it?
You need to know the circular length of your garden in order to be able to decide how many bricks to buy. Also, tires of vehicles are circular. If there is a particular distance that needs to be covered and if the rim of the tire is known, then it would be possible to calculate the number of rotations of the tire required to cover the distance.
It is not very difficult to learn how to find the circumference of a circle. With the formula and some practice one can easily calculate the rim of any circular object.