Knowing the kinetic energy formulas, you can compute the energy of a system in motion. In here, we provide and explain the rotational and relativistic formulas as well.
All of physics is the study of energy and its manifestations. When matter is at rest in a reference frame, the energy it contains, solely on behalf of its position, is termed as Potential Energy, while the energy it possesses when in motion, is termed as Kinetic Energy.
Definition
One of the most elusive concepts to grasp in physics is Energy. It takes various forms and everything that happens in this world is a subtle or major energy change. There is a formula for calculating it in every one of its forms.
Roughly put, kinetic energy is possessed by an object due its motion, relative to a frame of reference. It is the amount of work necessitated, to accelerate an object from its state of rest to a particular velocity. It is the extra amount of energy it acquires due to the work done in accelerating it. Being connected to motion, it always has a velocity component in its formula. The word ‘kinetic’ is aptly chosen, as it arises from the Greek word Kinesis, meaning motion.
There are two forms of mechanics that you will study. One is classical Newtonian mechanics and the other is relativistic mechanics. Relativistic mechanics supersedes Newtonian mechanics, which is now only useful when velocities of objects are much less than the speed of light.
Formula For Point Mass Or a Rigid Body
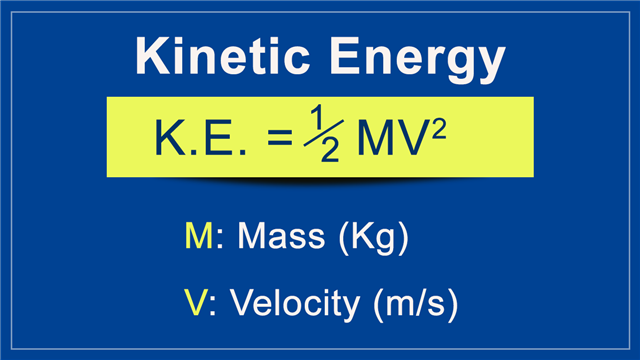
The formula for kinetic energy of a point mass or rigid body moving at non-relativistic speeds (speeds very less than speed of light) is the following:
Kinetic Energy (KE) = ½ M V2
Here, ‘M’ is the mass of the point mass (in Kg) or rigid body and ‘V’ is the velocity (m/sec) at which it is moving. The unit of energy is ‘Joule’.
Since linear velocity of the object is squared in the formula and mass appears as a linear term, its kinetic energy increases rapidly with rising velocity and increase in mass. More massive and speedier an object, more is the energy packed in.
Let me illustrate the usage of this formula with an example.
Consider that an object with a mass of 80 kg is moving at a speed of 40 km/s. To calculate the energy value of an object using the above formula, you will have to substitute the value of velocity and mass in the above formula. If you substitute these values,
Kinetic Energy of the Object = ½ x 80 Kg x 40 m/s x 40 m/s = 64000 Joules
As you can see, it is a simple matter of plugging in the values and calculating. The same formula can also be expressed in terms of momentum as:
Kinetic Energy = P2/2M
where P is the momentum of a body and M is its mass.
Rotational Kinetic Energy
If, rather than linear motion, the object is rotating, then the formula for kinetic energy presented above, is not useful. The formula is as follows:
Rotational Kinetic Energy = ½ I ω2
Here, ‘I’ is the ‘Moment of Inertia’ of the body and ‘ω’ is the ‘angular velocity’. To calculate the kinetic energy, you must calculate the moment of inertia of that body, along with its angular velocity.
Relativistic Kinetic Energy
If you are dealing with relativistic speeds, the kinetic energy formula, based on Newtonian mechanics will not be useful. The relativistic formula is as follows:
KErelativistic = mc2(γ – 1)
Where γ = 1/(√(1-v2/ c2), ‘c’ is the velocity of light, ‘m’ is the mass of the object, v is the velocity of object according to a reference frame, and ‘c’ is velocity of light. To calculate KE, just substitute values in this formula.
One book that might aid your understanding is the first volume of the Feynman Lectures on Physics, where the master physicist unplugs the subject and reveals its beauty.