This ScienceStruck article describes the specifics of velocity for an object in circular motion. The concept of tangential speed has been detailed, and the formula to calculate its value has also been specified.
Missing ‘radian’ from unit
While calculating tangential velocity as a product of the radius of its locus and the angular velocity, the product of radius and the angular displacement in radians gives the total arc distance traveled by the object in meters. This is the reason why the resultant unit is m/s and not m*rad/s.
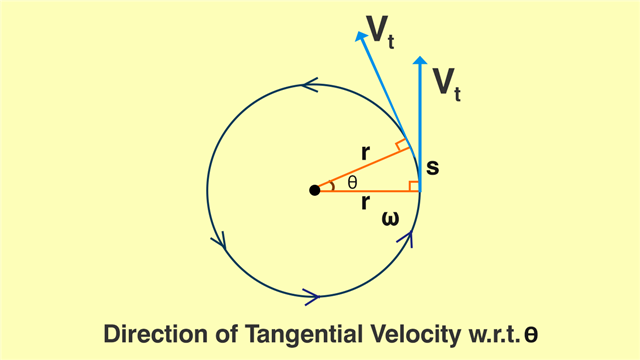
Tangential speed or tangential velocity can be defined as the linear speed of any object in motion following a circular path at any given instant of time. The direction of tangential speed can never be the same for any two instants of time for a given object in circular motion.
Let us consider an object in uniform motion along a continuous path, which is defined by a locus of points equidistant from a common point O. This path can be traced as a circle of radius r. If the total time taken to cover the entire path is taken to be T, each point on the circumference of this circle can be considered as an instant of time dt. At any such point, the linear direction of motion of the object will always be perpendicular to the radius of the circular path. The linear speed of the object in this direction for that point of time gives us the tangential velocity of the object. It is to be noted that the instantaneous value of angle dθ, through which the object has moved, is considered.
Calculating Tangential Velocity with Angular Velocity
Mathematically, tangential velocity is the product of the radius of the circular path and the rate of change of angle, i.e.,
Vt = r * (dθ/dt)
Now, it is known to us that the rate of change of angle gives the angular velocity of an object in circular motion. Therefore, angular velocity is given by,
ω = (θ/ t)
The angular velocity is represented by the unit, radians per second (rad/sec).
The value of angular velocity can be substituted in the equation for determining the tangential velocity. The substitution gives us the final formula for determining the value of tangential velocity, i.e.,
Vt = r * ω
Calculating Tangential Velocity with Arc Length
If the angular displacement or the angular velocity is not known, another formula is used for the calculation of the tangential speed. When the object has moved a complete circle, the value of circumference divided by the traveled time period t will give the value of tangential speed.
Mathematically,
Vt = (2*π*r)/t
We can also find the tangential speed if provided with the arc length S and the time of travel t. The arc length is the product of the angular displacement and the radius of the circle, i.e.,
S = r * θ
Therefore, the new formula for determining the tangential speed would be,
Vt = S/t
Tangential velocity is always measured in meters per second (m/s).
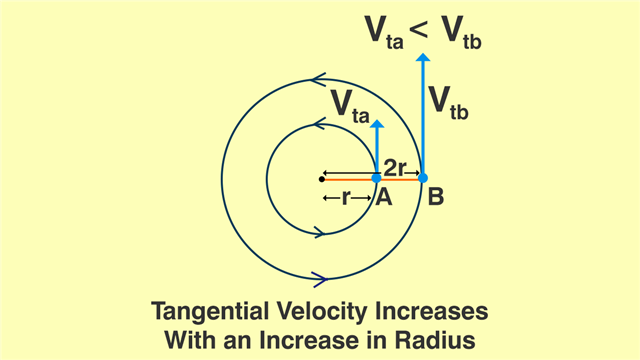
Effect of Radius on Tangential Velocity
Since the total angular displacement for each complete rotation along the circular path remains constant, the only factor that can affect the tangential speed is the radius of the circle. It can be observed from the formula itself that if the radius is increased, the tangential velocity correspondingly increases for the same time.
This can be best understood by tying two balls to a string such that one end of the string is still free. The string is swung in rotational motion such that both the balls attain a circular path. Now, both the balls have to complete one rotation in the same time period. The distance, however, is different for each of the moving balls since the circumference is not equal for the circular path they are following. In this manner, ball B has to travel more distance over the same specified time. It is then obvious that the speed of the ball B has to be greater than A. Hence, we can conclude that tangential velocity of an object increases linearly with an increase in the radius of the circular path being followed.
Evidently,
[Vta = (2*π*r)/t] < [Vtb = (2xπ*2r)/t]
It becomes clear that the tangential speed of an object increases as it moves away from the center of the orbit in which it was rotating.
Both tangential speed and tangential velocity mentioned in this article are one and the same thing, and represent the magnitude of speed only, not its direction. The objects under study were considered to be in uniform circular motion. Any change in velocity with respect to time would result in tangential acceleration.