The area under a stress-strain curve represents toughness of a material. We provide you with information that will help you find area under a stress-strain graph.
Basic Difference
Strain is said to be dimensionless with no units because it stands for relative change, while stress has dimensions and comes with units.
Elasticity is the property of a solid material to resist deformation. In other words, it is the property of a material to return to its original shape and size after the external deforming forces that were stretching or compressing it have been removed.
When the external deforming forces are applied to a body, what resists the deformation are the internal restoring forces within the body. As soon as the external deforming forces are removed, these internal restoring forces spring to action and bring back the body to its original shape.
Stress: The internal restoring force per unit cross-sectional area of a body is defined as stress. This internal restoring force is equal to the external deforming force applied to the body, per unit area at equilibrium. It is calculated as:
σ (stress) = F (force)/A (Area)
Strain: When an external deforming force is acting on a body, its shape changes. This change in the shape of the body with respect to the original shape is defined as strain.
Strain = Extension/Length = △ L/L
The relationship between stress and strain is given by Hooke’s law, which states that within elastic limit, the stress inflicted on a body is directly proportional to the strain caused on it.
Stress/Strain = Constant = Modulus of elasticity
Graph of Stress Vs. Strain
The stress-strain graph of a material represents the relationship between the stress and strain under different conditions. It is drawn by plotting the corresponding strain of a material when subjected to a particular stress. The load on the specimen is increased in increments gradually, and the corresponding elongation in the length is recorded. The graph with the stress on the Y-axis and strain on the X-axis is the stress-strain diagram.
Let’s examine the stress-strain curve for a particular metal.

▶ The X-axis represents the strain produced.
▶ The Y-axis represents the stress, i.e., the force applied to the specimen.
✦ Initially, the graph is a straight line because as the load on the specimen increases, the extension on it also increases. This means that stress and strain are in direct proportion to each other.
✦ Now, after a limit is reached, the graph becomes non-linear because the elastic limit is reached. So within an elastic limit, Hooke’s Law is obeyed.
✦ The elastic limit is the limit after which the material will no longer go back to its original shape and size; it is the maximum stress that the material can withstand without producing permanent deformation in it. But when a material is subjected to stress beyond its elastic limit, it experiences permanent deformation.
✦ The region in the stress-strain graph from the origin to the elastic limit is called the elastic range, and the region beyond the elastic limit is called the plastic range.
✦ Yield point is that point on the stress-strain curve beyond which the material will yield itself, i.e., it will have a considerable deformation without a considerable increase in load.
✦ Another point worth noting on the stress-strain graph is the ultimate strength or the tensile strength. This point is the maximum y coordinate on the graph.
✦ Rupture strength is the strength that the material possesses when it ruptures or finally breaks.
Toughness
When a material is subjected to load, it absorbs energy that is applied to it. The ability of a material to absorb energy and undergo plastic deformation without permanently fracturing is the toughness of the material. Toughness is the amount of energy per unit volume that a material can absorb without fracturing.
Calculating toughness from a stress-strain curve
Toughness can be calculated by finding the area under a stress-strain curve drawn for that material.
Calculating Area Under the Stress-Strain Curve
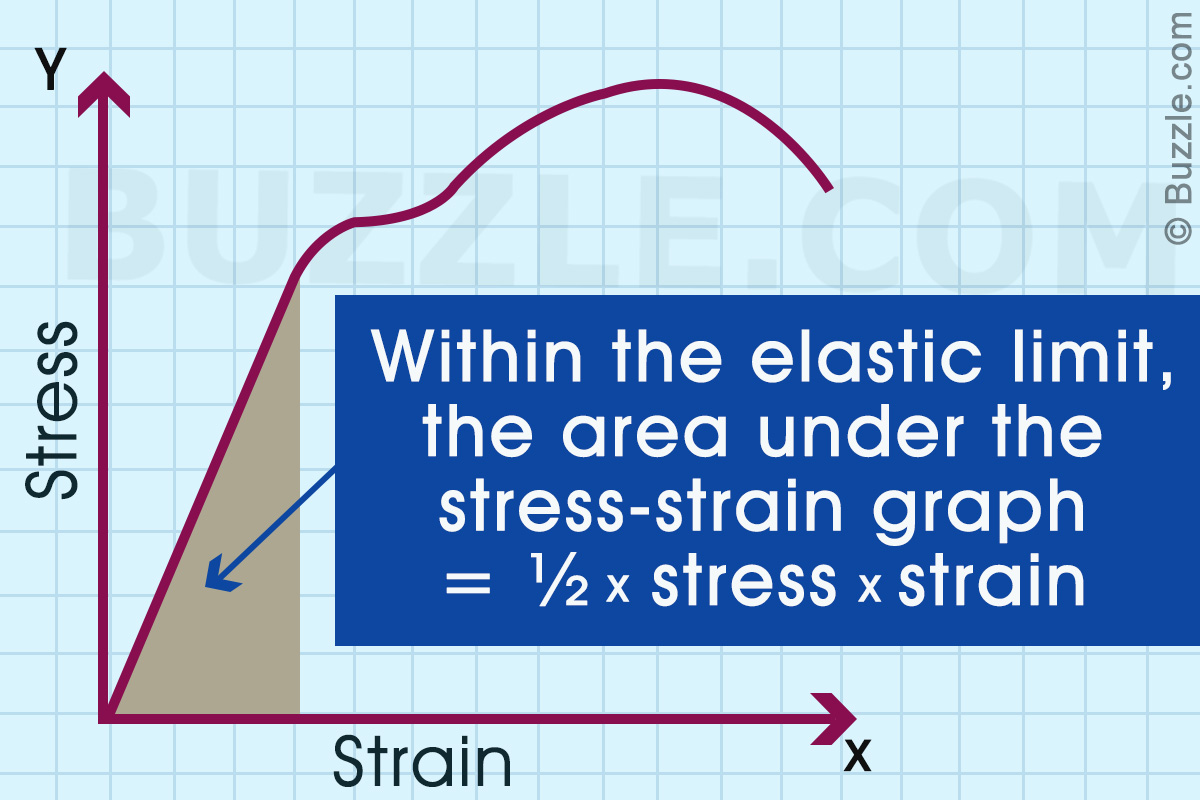
✦ The area under a stress-strain curve can be calculated by integrating the curve. Where the graph is a straight line, you will have a triangular region, the area of which can be easily found out.
The area under the stress-strain graph is the strain energy per unit volume (joules per metre3).
Strain energy per unit volume = 1/2 stress x strain
Hence, Area = 1/2 stress x strain
✦ Where the graph is a curve, you will have to find out the equation of the curve and then integrate the curve within the limits of the graph. The following formula is used.

where f(x) is the function that the graph represents, and the limits of the graph are given by a and b.