No part of math is more confusing than geometry. The main reason being the numerous terms which students get entangled in. In this ScienceStruck post, we give you a list of the basic terms used in geometry, to make understanding this branch of mathematics easier.
Did You Know?
The word ‘Geometry’ comes from the ancient Greek words ‘geo’ and ‘metron’, that mean earth and measurement respectively.
Geometry can be called a study of the shape, size, and position of objects. It is considered to be difficult due to the many terms used in the subject, and also due to the fact that one has to understand the subject; it cannot be learned by rote. Most of these terms can be confusing to students, and in addition to these terms, there are various theorems, laws, and definitions that have to be understood as well.
In this article, we have given you a list of the definitions of some of the basic terms used in geometry. It should be noted that neither is this list for beginners, not is it for advanced students. It is meant to be a ready reference for those who have studied geometry earlier.
List of Basic Terms Used in Geometry
Acute Angle

If the angle formed by two lines intersecting is less than 90°, then the angle is known as acute angle.
Acute Triangle

An acute triangle can be defined as a triangle where all the 3 angles that make up the triangle measure less than 90° each.
Altitude

The altitude of a triangle is a line segment that connects a vertex to the opposite line of the triangle, and is perpendicular to that line.
Angle

When two line segments intersect or have a common end point, then the inclination of one line with the other is called an angle. Angles are measure in degrees.
Angle-Angle-Angle (AAA) Similarity

The angle-angle-angle (AAA) similarity test says that if two triangles have corresponding angles that are congruent, then the triangles are similar.
Angle Bisector

A ray, that divides any angle into exactly half, making two equal angles in the process, is known as an angle bisector.
Arc of a Circle

An arc of a circle is a connected section of the circumference of a circle. Arcs are measured in two ways: as the measure of the central angle, or as the length of the arc itself.
Central Angle

A central angle is defined as one which has its vertex at the center of a circle.
Centroid

The meeting point of the three medians of a triangle is called the centroid. This point is the center of mass of the triangle.
Circle

A circle can be defined as the set of all points in a plane that are equidistant from a given point in the plane, which is the center of the circle.
Circumcenter

The meeting point of the three perpendicular bisectors of a triangle is known as its circumcenter. This point is equidistant from the three vertices of the triangle.
Circumference

The circumference of a circle is said to be the length of the boundary or the border of a circle.
Concave Polygon

Any polygon that has at least one angle that measure more than 180° is called a concave polygon. Such polygons look like they have one or more angles caved in.
Concurrent

When three or more lines meet at a single point, they are said to be concurrent. The three medians, three perpendicular bisectors, three angle bisectors, and three altitudes of a triangle are each concurrent.
Cone

A cone is a three-dimensional figure with a single base tapering to an apex.
Congruent

Two figures are said to be congruent if their corresponding lengths are the same, and the measure of their corresponding angles are same. Such figures are generally said to be the same shape and size.
Congruent Triangles

Congruent triangles are triangles that have the same size and shape. In particular, corresponding angles have the same measure, and corresponding sides have the same length.
Converse

Converse means the “if” and “then” parts of a sentence are switched. For example, “If two numbers are both even, then their sum is even” is a true statement. The converse would be “If the sum of two numbers is even, then the numbers are even,” which is not a true statement.
Convex Polygon

A convex polygon is any polygon that is not concave, or where none of the angles measure more than 180°.
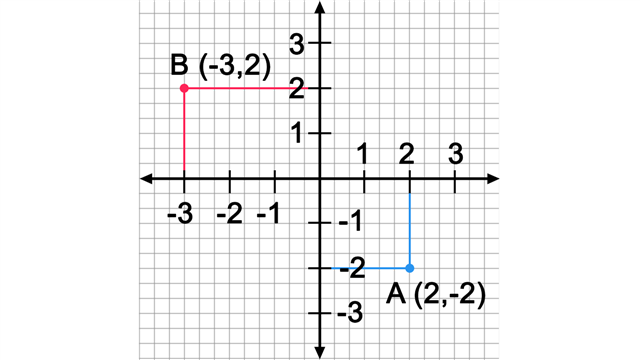
Coordinates
The coordinates of a point describe where it is located with respect to the x- and y-axes. The form (x,y) is a standard convention that allows everyone to mean the same thing when they reference any point.
Cosine

If A is an acute angle in a right angle triangle, then the cosine of A is defined as the length of the side adjacent to angle A, divided by the length of the hypotenuse of the triangle. This is written as cos A = (adjacent)/(hypotenuse).
Cross Section

The face obtained after making a slice through an object is known as the cross section of that object.
Diameter

A segment that passes through the center of the circle, and has its endpoints on the circle, is referred to as the diameter of the circle.
Edge

A line segment where two faces of an object intersect is known as an edge.
Equilateral Triangle

A triangle where the length of all its three sides are equal is known as an equilateral triangle.
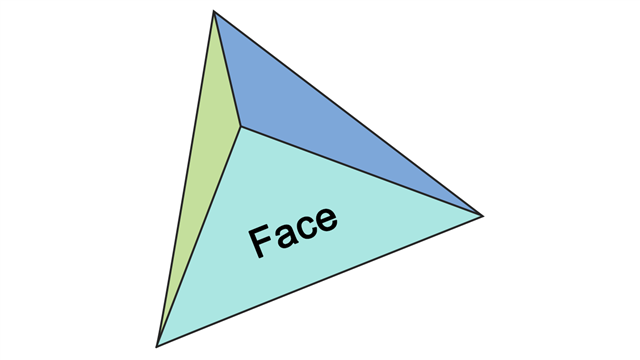
Face
A face is a polygon by which a solid object is bound. For example, a cube has six faces, with each face being a square.
Frieze Pattern
A frieze pattern is an infinite strip containing a symmetric pattern.
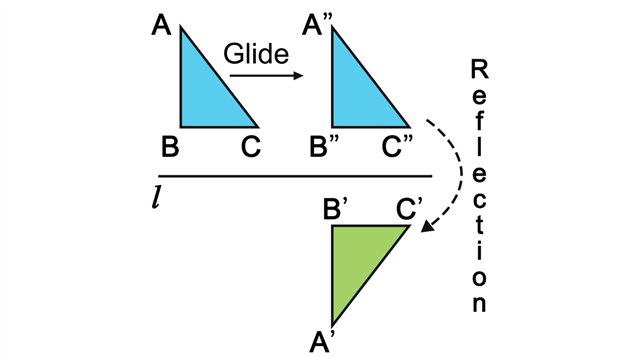
Glide Reflection
A glide reflection is a combination of two transformations: a reflection over a line followed by a translation in the same direction as the line.
Hypotenuse

In a right angle triangle, the side of the triangle that is opposite to the right angle, is called the hypotenuse.
Incenter

The meeting point of the three angle bisectors of a triangle is known as its incenter. The incenter is equidistant from each of the three sides of the triangle.
Inscribed Angle

An angle whose vertex lies on the circle, and rays intersect the circle is called an inscribed angle.
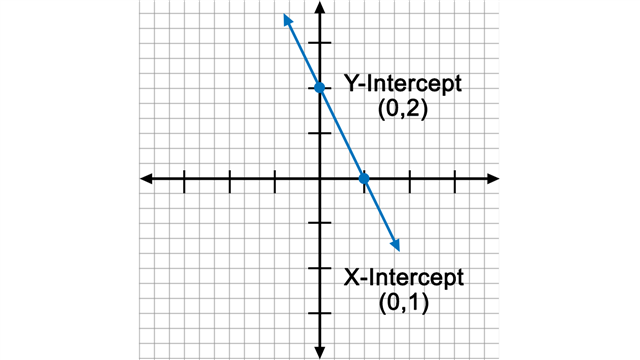
Intercept
In geometry, an intercept is defined as an intersection of a graph with one of the axes. An intersection with the horizontal axis is referred to as an x-intercept, and an intersection with the vertical axis is referred to as a y-intercept.
Irregular Polygon

An irregular polygon is any polygon that is not regular, or a polygon where none of te sides or angles are equal.
Isosceles Trapezoid

An isosceles trapezoid is a quadrilateral with one pair of parallel sides and congruent base angles, or it is a trapezoid with congruent base angles.
Isosceles Triangle

An isosceles triangle is a triangle where the length of any two sides equal are equal.
Kite

If two pairs of adjacent sides in a quadrilateral have equal length, then it is called a kite.
Line

A line can be defined as having only one dimension: length. It continues forever in two directions (so it has infinite length), but it has no width at all. A line connects two points via the shortest path, and then continues on in both directions.
Line Segment

The part of a line that lies between two points is called a line segment. Line segments have a finite length and no width.
Line Symmetry or Reflection Symmetry

An object is said to have line symmetry, or reflection symmetry, if it can be folded in half along a line so that the two halves match exactly. This folding line is called the line of symmetry.
Median

A segment that connects any vertex of a triangle to the midpoint of the opposite side is called a median.
Midline

A midline is a segment that connects two consecutive midpoints of a triangle.
Midline Theorem

The midline theorem states that a midline of a triangle creates a segment that is parallel to the base and half as long.
Net
A net is a two-dimensional representation of a three-dimensional object.
Obtuse Angle

If the angle formed by the intersection of two lines is more than 90°, then the angle is known as obtuse angle.
Obtuse Triangle

An obtuse triangle is a triangle where at least one angle measures more than 90°.
Orthocenter

The orthocenter of a triangle is the point where the three altitudes meet, making them concurrent.
Parallel Lines

Parallel lines are two lines in the same plane that never intersect. No matter where you measure such lines, their perpendicular distance is always constant.
Parallelogram

A parallelogram is a quadrilateral that has two pairs of opposite sides that are parallel.
Perpendicular Bisector

The perpendicular bisector of a line segment is perpendicular to that segment and bisects it; that is, it goes through the midpoint of the segment, creating two equal segments.
Plane

A plane is a flat, two-dimensional object. A plane must continue infinitely
in all directions and have no thickness at all. It can be defined by two intersecting lines or by three non-collinear points.
Platonic Solid

A Platonic solid is a solid such that all of its faces are congruent regular polygons and the same number of regular polygons meet at each vertex.
Point
A point can be defined as having only location; it has no length, width, or depth.
Polygon

A polygon is a two-dimensional geometric figure made of straight line segments, where each segment touches exactly two other segments, one at each of its endpoints. A polygon divides the plane into two distinct regions, the inside and the other outside the polygon.
Polyhedron

A polyhedron is a closed three-dimensional figure, where all the faces are made up of polygons.
Prism

A prism is a solid that has parallel congruent bases which are both polygons. The bases must be oriented identically. The lateral faces of a prism are all parallelograms or rectangles.
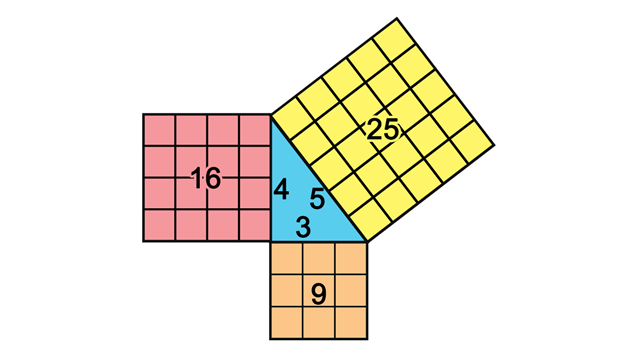
Pythagorean Theorem
The Pythagorean theorem states that if you have a right triangle, then the square built on the hypotenuse is equal to the sum of the squares built on the other two sides.
Quadrilateral

A quadrilateral is a polygon with exactly four sides.
Radius

The radius of a circle is the distance from the center of the circle to a point on the circle, and is constant for a given circle.
Ray

A ray is a line that has a point on one end, and extends infinitely in the other direction.
Rectangle

A rectangle is a quadrilateral with four right angles.
Reflection

Reflection is a rigid motion, where an object changes its position but not its size or shape, due to the creation of a mirror image of the object.
Regular Polygon

A regular polygon has sides that are all the same length and angles that all measure the same.
Rhombus

A rhombus is a quadrilateral that has all four sides congruent.
Right Angle

If two lines intersect at an angle of 90°, then the angle formed is said to be a right angle.
Right Angle Triangle

A right angle triangle is a triangle where at least one angle measures 90°.
Rotation
Rotation is a rigid motion, meaning an object changes its position but not its size or shape. In a rotation, an object is turned about a “center” point, through a particular angle.
Rotation Symmetry

A figure has rotation symmetry if you can rotate (or turn) that figure around a center point by fewer than 360° and the figure appears unchanged.
Scalene Triangle

A scalene triangle is a triangle where all three sides have a different length.
Sector of a Circle

A sector of a circle is a part of the interior of a circle bounded by two radii and an arc.
Side-Angle-Side (SAS) Congruence

Side-angle-side (SAS) congruence states that if any two sides of a triangle are equal in length to two sides of another triangle, and the angles between each pair of sides have the same measure, then the two triangles are congruent; that is, they have the same shape and size.
Side-Angle-Side (SAS) Similarity

The side-angle-side (SAS) similarity test says that if two triangles have two pairs of sides that are proportional, and the included angles are congruent, then the triangles are similar.
Side-Side-Side (SSS) Congruence

The side-side-side (SSS) congruence states that if the three sides of one triangle have the same lengths as the three sides of another triangle, then the two triangles are congruent.
Side-Side-Side (SSS) Similarity

The side-side-side (SSS) similarity test says that if two triangles have all three pairs of sides in proportion, the triangles must be similar.
Similar

Two objects are said to be similar if their corresponding angles have the same measure and their corresponding sides are in proportion.
Similar Triangles

Two objects are said to be similar if their corresponding angles have the same measure and their corresponding sides are in proportion.
Sine

If angle A is an acute angle in a right angle triangle, the sine of A is the length of the side opposite to angle A, divided by the length of the hypotenuse of the triangle. This is written as A = (opposite)/(hypotenuse).
Supplementary Angles

Supplementary angles are two angles that add up to 180°.
Square

A square is a regular quadrilateral, or an object where all the four sides are equal.
Symmetry

A design has symmetry if you can move the entire design by either rotation, reflection, or translation, and the design appears unchanged.
Tangent

If angle A is an acute angle in a right angle triangle, the tangent of A is the length of the side opposite to angle A, divided by the length of the side adjacent to angle A. We write this as tan A = (opposite)/(adjacent).
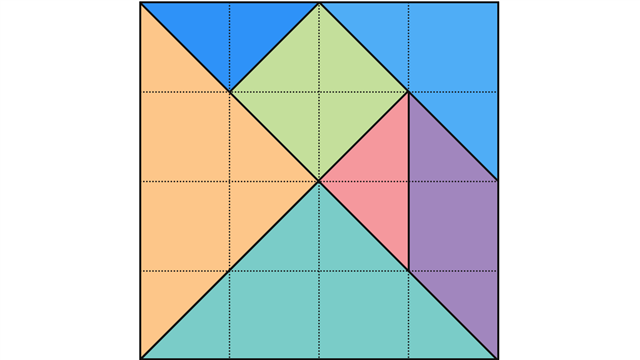
Tangram
A tangram is a seven-piece puzzle made from a square, that contains two large
isosceles right triangles, one medium isosceles right triangle, two small isosceles right triangles, a square, and a parallelogram.
Theorem

A theorem in mathematics is a proven fact. A theorem about right triangles must be true for every right triangle; there can be no exceptions. Just showing that an idea works in several cases is not enough to make an idea into a theorem.
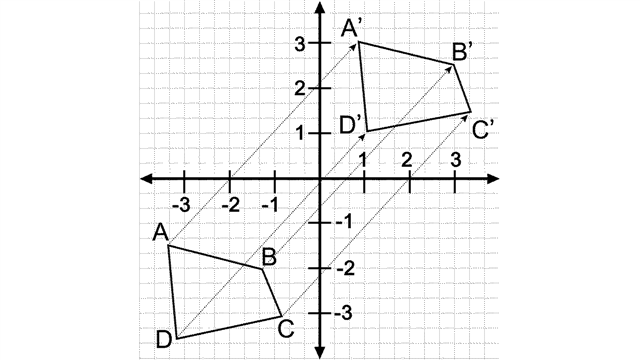
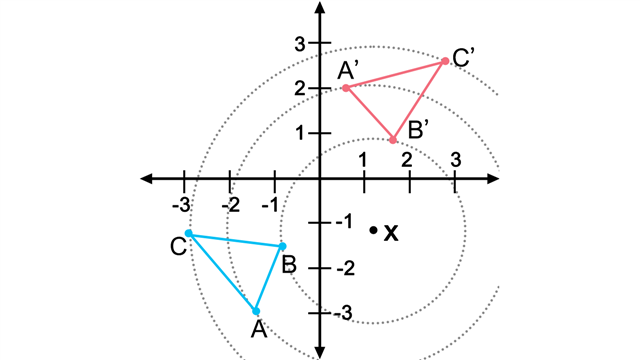
Translation
Translation is a rigid motion, meaning an object changes its position but not its size or shape. In a translation, an object is moved in a given direction for a particular distance. A translation is, therefore, usually described by a vector, pointing in the direction of movement and with the appropriate length.
Translation Symmetry

Translation symmetry can be found only on an infinite strip. For translation symmetry, you can slide the whole strip some distance, and the pattern will land back on itself.
Transversal

A transversal is a line that passes through (transverses) two other lines.
Trapezoid

A trapezoid is a quadrilateral that has one pair of opposite sides that are parallel.
Triangle Inequality

The triangle inequality says that for three lengths to make a triangle, the sum of the lengths of any two sides must be greater than the third length.
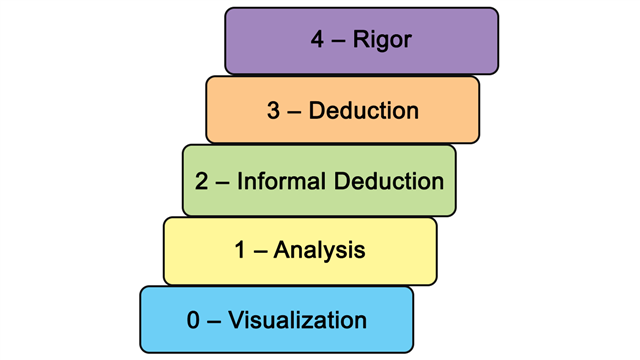
Van Hiele Levels
Van Hiele levels are a theory of five levels of geometric thought. The levels are (0) visualization, (1) analysis, (2) informal deduction, (3) deduction, and (4) rigor.
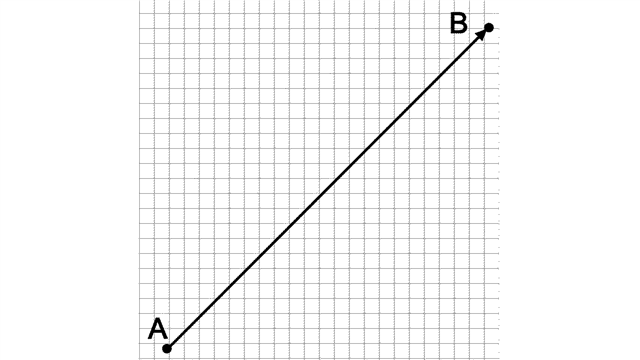
Vector
A vector can be used to describe a translation. It is drawn as an arrow. The arrowhead points in the direction of the translation, and the length of the vector tells you the length of the translation.
Venn Diagram

A Venn diagram uses circles to represent relationships among sets of objects.
Vertex

A vertex is the point where two sides of an object meet.
There are about a hundred other geometry terms which are mostly derivatives of the terms discussed above. Once you are thorough with these basic terminologies, it is not difficult to understand the other terms and definitions in geometry.