Every macroscopic and microscopic body or object in the universe exerts different forces on the surroundings, as well as experiences the effect of various forces on it. It is possible to study such physical entities with the help of a free body diagram. Read this ScienceStruck article to gain more information about this concept.
Fast Fact
The free body diagram of a car traveling at a constant speed consists mainly of five forces, when considered in an actual situation. These vectors are that of friction, gravity, normal force, air resistance, and engine driving force. In a hypothetical situation without external forces (friction and air resistance), only the three remaining forces will act on the vehicle.
A free body diagram is defined as an illustration that depicts all the forces acting on a body, along with vectors that are applied by it on the immediate environs. Apart from the acting forces and subsequent work done, the moment magnitudes are also considered to be a part of such diagrammatic representations. These diagrams are then used to calculate these forces, estimate their directions, and also to thoroughly analyze them. One should keep in mind that these representations only consist of vector quantities, and scalars like distance and speed are not to be drawn in the diagrams.
Problems regarding physics-, statistics-, and engineering-related studies are often solved using this concept. In physics, these illustrations have immense importance, as they convert materialistic parameters to non-materialistic or theoretical ones, thereby aiding in simplification. They can be rough sketches as well as freehand drawings, and it is not necessary to draw them to the scale of the actual bodies. The objects that are characterized by such forces might be of three types: rigid, non-rigid, and particles. They are used for modeling of the concerned objects in physics- and engineering-related studies.
INDEX
► Explanation
► How to Draw
► Examples
► Practice Problems
Explanation
Free body diagrams are always represented in the form of two-dimensional figures, which consist of the ‘X’ and ‘Y’ axis. In classical mechanics, 3D representations are not preferred at least at the basic level, to maintain simplicity for solving problems. The three main aspects that need to be considered in drawing these diagrams are: the direction of the force, the magnitude of the force, and the origin/source/application point of the force. Given below are the main types of forces that can act on a body in any given circumstances.
Types of Forces
Applied Force
This vector is applied to cause a change in the state of the body (in terms of rest or motion), along with an effect on other objects, surfaces, or mediums. Its magnitude depends on the action of all the other forces, and in some instances, more than one applied force may be present. When this force is exerted, work is done by the body.
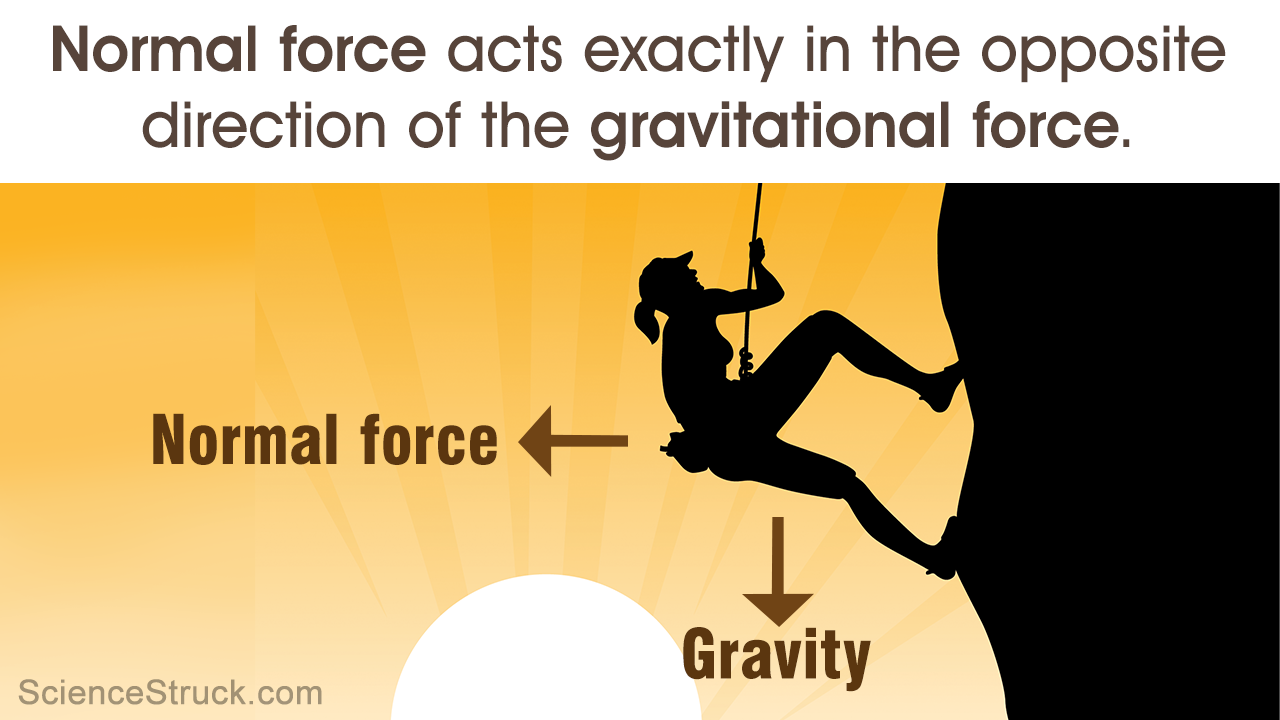
Normal Force
It acts in exactly the opposite direction as that of the gravitational force, and perpendicular to the surface. In most cases, the surfaces are shown to be horizontal, and hence, the normal force can be said to act in the upward direction. Simply said, it is the force exerted by the surface on which the body rests, to counter gravity.
Gravitational Force
According to Newton, every object attracts every other object with a force that is directly proportional to the product of their masses, and inversely proportional to the square of distance between them. Thus, any object on land, air, water, or even space will experience some effect of gravity. Its direction is opposite to that of the normal force. On our planet, the average value of gravitational attraction is about 9.8 m/s2.
Frictional Force
This vector acts in the opposite direction to the applied force, and exists because of some discrepancies present on the surface of contact with the body. Though its magnitude is mostly small as compared to the applied force, it can cause the opposite effects as compared to those of the applied force on the body, thus slowing it down (deceleration). Smoother the surface, less will be the friction.
Tensional Force
It exists when an object is stretched or deformed from its original shape and structure. This vector may be influenced by an additional applied force and gravity. Many complex free body diagrams exhibit such vectors, and tensional forces are often accompanied with stress and strain of a body. This might include temporary or permanent deformation of the body.
Air Resistance/Drag
In case an object is in motion in the air, it shows the presence of air resistance, which acts in the opposite direction as that of the applied force. This vector is also called drag, which can act on the back-end of the body in motion. It is a type of friction, which exists mainly due to the relative movement of the body with respect to the air current movements.
Refer to the following figures to understand all the forces on an object.
Figure 1

A box is being shifted on a horizontal surface towards the right. Thus, the applied force is towards the right, whereas, the frictional force is towards the left. The weight acts in the downward direction due to the effect of gravitational force, while the normal force acts in the upward direction, opposite to gravity.
Figure 2

The diagram above shows the same box, but on an inclined surface. Thus, the force of gravity will be acting in multiple directions; at an angle to the surface, as well as perpendicular to the surface. The angle of the ramp is 30 degrees. If we assume that the box is accelerating towards the slope bottom, then ‘Fa’ can be said to be equal to ‘mgsinθ’, whereas, the gravitational force perpendicular to the inclined surface is equal to ‘mgcosθ’. In these terminologies, ‘m’ is the mass and ‘g’ is gravitational acceleration.
How to Draw a Free Body Diagram
Learning to draw a free body illustration is very important, especially for those who are into engineering, physics, mechanical studies, and other related fields. This technique can be further utilized for any new technology present at the concept level, which is prominently seen in the field of automobiles.
When you draw these diagrams, you first have to recognize the various kinds of forces that are acting on the object. After this, note down their directions, along with the respective symbols. Then, you can draw any representative geometric figure like a square, circle, or a rectangle, etc., along with all the particular force directions in the form of arrows. The labellings and values, if present, can also be written. In the final step, describe all the forces briefly in order so that you clearly understand the entire diagram. Mostly, if a single body is concerned, all the forces will coincide at the center of gravity of that object.
One important thing to keep in mind is to draw the arrow lengths as per the force magnitude. Also, the net vector for two or more forces acting in different directions is not to be drawn; they can be represented as separate ones. An ‘X’ and ‘Y’ axis is also drawn sometimes so that the orientation of vectors with respect to horizontal and vertical directions can be shown. These axes are either connected to the central point of the diagram, or can be present toward one side.
The following images will show you the method to draw a free body diagram, with the help of a simple example.

The first image shows two rugby players who are fighting for the ball and collide with each other. In scientific terms, both are moving toward each other, and hence, the forces that cause their motion are originating from two different points. All the forces that are mentioned in the above section act on these players, and hence, their free body diagram might be a little complicated.

In the second image, draw all the forces that are acting on the concerned bodies. Thus, both experience gravity, and this is indicated by a downward arrow (Fg). The applied forces of both the players are indicated as ‘Fa’, and the normal forces are indicated as ‘Fn’. Now, as this is a realistic situation, we cannot ignore externally active forces like friction (Ff). This can be observed at the players’ feet, and is characterized by a direction that is exactly opposite to the applied force. The point of contact between both individuals is supposedly the center of mass of the entire scenario.

In the third and final image, instead of the player silhouettes, draw two geometric shapes like rectangles, with all the forces, labellings, values, names, directions, etc., all shown in the image. Thus, this is called the free body diagram, which is the final output of this concept.
Examples of Free Body Diagrams
It is easier to solve problems of free body diagrams based on examples, rather than any random hypothetical bodies that appear in geometric shapes. This is because, everyone can relate to real-life instances better than theoretical ones.
Example 1: A commercial passenger airplane is flying with a constant speed and heading towards west.

This indicates that, apart from an applied force (thrust), gravity is also acting on the airplane in the downward direction (weight). As it is flying in the air, in realistic conditions, the plane will experience some drag at the tail end, as well as air resistance (lift). The former acts exactly in the opposite direction as that of thrust, whereas, the latter acts in the upward direction. The orientation of forces without the actual body is also shown at the top-right corner.
Example 2: A sprinter is heading towards east on a running track.

In this case, instead of air resistance, a normal force (ground reaction force) will be acting on the sprinter’s body, which will be exactly equal and opposite to the force or weight of the body on the ground surface (from Newton’s third law of motion). A small drag will be present if wind currents are flowing in the opposite direction as that of the sprinter. Also, the frictional force acts in the opposite direction to the applied force at the point of contact between the body and surface, i.e., on the shoe soles.
Example 3: A cyclist is moving up an incline on a ramp, which has an angle of 30 degrees with the su

In this situation, the surface is not horizontal, and hence, the forces acting differ a bit as compared to a body moving on a flat surface. The gravitational forces are acting in three different directions on the cyclist, which are: perpendicular to the inclined surface, perpendicular to the ground surface, and in the opposite direction of the applied force. Other vectors are also present, but the directions are different as compared to the examples above.
Example 4: A person is operating a lawn mover on the ground surface.

In this case, the applied force is at an angle of 30 degrees to the horizontal ground surface. Along with this, all the four main forces are acting on the man as well as on the lawn mover (F applied, F gravity, F friction, F normal). If only the device is considered, then the free body diagram consists of one representation. It will be a combined diagram, in case both man and machine are included for observation.
Practice Problems With Answers
For a better understanding of the subject, solve these problems by sketching the free body diagrams of the mentioned objects. You can also come up with your own type of problems and questions, by combining various examples which will help in generating complex diagrams.
Problem 1
A book placed on the table is pushed towards the left with acceleration. Draw the force diagram of this instance. Do not take air resistance into account.
Answer :

Problem 2
A small child moves down a slide in a park with constant speed. Sketch the free body diagram of this action, if the angle of the slide with the ground surface is 40 degrees. Do not ignore frictional forces.
Answer :

Problem 3
A flying squirrel leaps from a tree and glides for some distance toward the left, before reaching another branch. Sketch a diagrammatic representation of any physical entities that might be acting on it while it is in air.
Answer :

Problem 4
Three boxes are stacked one on top of each other, with their sizes and weights in the descending order from bottom to top. Each exerts a weight on the box below. Construct the illustration that represents the forces and weights acting on all the bodies mentioned.
Answer :

Problem 5
On an incline having an angle of 30 degrees with the horizontal, a sack is moved up the slope with the help of a pulley attached to the upper end of the sack. Draw the free body diagram by representing the various forces acting on the sack, as well as the pulley. External forces are also acting, in this case.
Answer :

In order to draw these diagrams flawlessly, one must have good knowledge of physics and mathematics, at least on a basic level. Nowadays, such illustrations can be digitally obtained instead of sketching them, as various software for the same are available. After feeding in the data, an automatic set of diagrams can be generated.