Type 1 and type 2 errors are both methodologies in statistical hypothesis testing that refer to detecting errors that are present and absent. The following ScienceStruck article will explain to you the difference between type 1 and type 2 errors with examples.
Quick Fact
Used extensively for statistical hypothesis testing, type 1 and type 2 errors find their applications in engineering, mechanics, manufacturing, business, finance, education, medicine, theology, psychology, computer security, malware, biometrics, screenings, and many more.
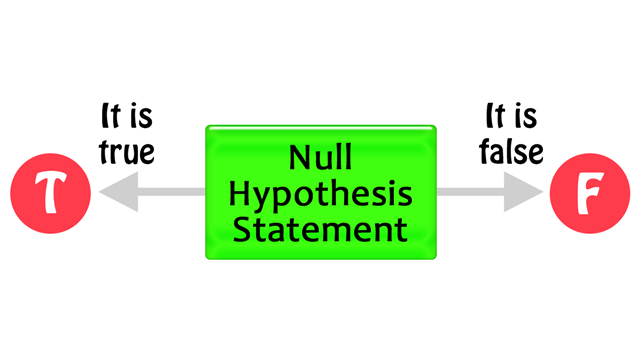
A hypothesis is something that does not exist. To be clear, a hypothetical situation is something that one needs to imagine, in order to join the dots and arrive at a conclusion. The term ‘null hypothesis’ can be defined as a statement that produces no effect. A statement that opposes this statement can be termed as ‘alternative hypothesis’.
The acceptance and rejection of the null hypothesis is done by means of the type 1 and type 2 errors. The interpretation of both these terms differ with various disciplines and is a matter of debate among experts. The type 1 vs. type 2 errors comparison outlined below along with suitable examples will help you understand this concept better.
Diagrammatic Representation
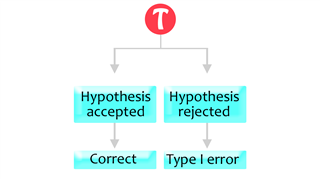
Type 1 Error
- It occurs when a null hypothesis is rejected when it is actually true.
- In other words, it occurs when we try to find out something that does not possibly exist at all.
- It is also called ‘false positive’ or ‘alpha error’.
- It indicates the acceptance of the alternative hypothesis.
- So, ultimately, what happens is that the true null hypothesis is wrongly rejected even if it is true.
Examples
- Suppose you decide to bake lasagna, and you add an extra ingredient (assuming it will enhance the taste), that is actually not supposed to be added.
- In this case, the truth of taste improvement in the dish is tested. Therefore, the null hypothesis would be ‘Adding this ingredient has no effect on the taste’.
- Contrary to this, if your dish tastes great, it would automatically be assumed that it is so because of the extra ingredient, when in reality, it is not.
- Therefore, the null hypothesis is true in this case, but is being rejected due to false effect.
- Another example would be to consider the trial of a person accused of murder.
- The null hypothesis would be a statement, like ‘He is innocent’.
- If it is true, he will be let free, and it will be the correct decision. If he is convicted for something he has not done, a type 1 error has occurred.
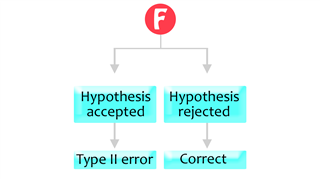
Type 2 Error
- It occurs when a null hypothesis is not rejected when it is actually false.
- In other words, it occurs when we try to ignore something that actually exists.
- It is also called ‘false negative’ or ‘beta error’.
- It indicates the failure of being able to accept the alternative hypothesis.
- What ultimately happens here is that the true null hypothesis is wrongly accepted even if it is false.
Examples
- Consider the same examples as above for convenience.
- In this case, you have to false null hypothesis, i.e., the statement is ‘Adding this ingredient has no effect on the dish’, when in reality, it will have some effect on the dish, good or bad.
- So, let’s say, the overall consensus is that the dish will be the same as before, but since the hypothesis is false, the dish has a slightly spicier taste.
- Now, this change will not be accepted by any of your guests, they would vouch that the dish is the same as before, and attribute the spicier taste to some other factor.
- Thus, here the null hypothesis is false, but it is being accepted.
- Similarly, let the null hypothesis ‘He is innocent’, be false in the second example, i.e., the man is actually guilty.
- Thus, if the statement is false, and the man is convicted, it will be the right decision, but if the man is left free despite having done the crime, a type 2 error has occurred.
- In this scenario, we fail to accept what is true.
Factors of Differentiation
| Type 1 Error | Type 2 Error |
| Medicine | |
| Indication that a person carries a deadly virus, when in reality, he does not. Or the notion that a particular drug has cured a disease, when in reality, the drug has had no effect on the patient. | Accepting that the person does not carry any deadly infection, in reality, he does carry a virus. Or, a drug has cured a particular disease, but is not accepted to be effective against the same. |
| Computer Security | |
| Authentic users may be classified as hackers. | Hackers/imposters are accepted as authorized users. |
| Biometrics | |
| Possibility of rejection even with an authorized match. | Possibility of acceptance even with a wrong/unauthorized match. |
| Security Screening | |
| Items that are not dangerous may also be rejected. | Items that are definitely dangerous may also be accepted. |
| Research | |
| Rejection is based on a particular difference in calculation, but in reality, there is no difference. | The research is accepted even if there is a difference in calculation, assuming there isn’t any. |
| Finance | |
| High quality goods are rejected by the automated inventory system. | Low quality goods are accepted by the automated inventory system. |
Both, type 1 and type 2 errors are important and need to be taken into consideration in all fields, especially while calculating them in the fields of mathematics and science. These errors can be avoided by means of replication and adjusting the significance levels. The two terms should be accurately understood and not confused with each other, because in case of medical screenings and other vital applications, an in-depth knowledge is necessary to make the correct decision.