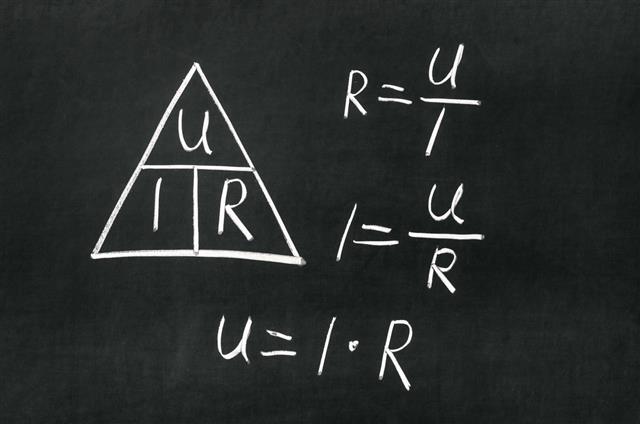Learning physics is all about applying concepts to solve problems. This article provides a comprehensive physics formulas list, that will act as a ready reference, when you are solving physics problems. You can even use this list, for a quick revision before an exam.
Physics is the most fundamental of all sciences. It is also one of the toughest sciences to master. Learning physics is basically studying the fundamental laws that govern our universe. I would say that there is a lot more to ascertain than just remember and mug up the physics formulas. Try to understand what a formula says and means, and what physical relation it expounds. If you understand the physical concepts underlying those formulas, deriving them or remembering them is easy. This ScienceStruck article lists some physics formulas that you would need in solving basic physics problems.
Physics Formulas
- Mechanics
- Friction
- Moment of Inertia
- Newtonian Gravity
- Projectile Motion
- Simple Pendulum
- Electricity
- Thermodynamics
- Electromagnetism
- Optics
- Quantum Physics
Derive all these formulas once, before you start using them. Study physics and look at it as an opportunity to appreciate the underlying beauty of nature, expressed through natural laws. Physics help is provided here in the form of ready to use formulas. Physics has a reputation for being difficult and to some extent that’s true, due to the mathematics involved.
If you don’t wish to think on your own and apply basic physics principles, solving physics problems is always going to be tough. Our physics formulas list is aimed at helping you out in solving problems. The joy of having solved a physics problem on your own, is worth all the effort! Understanding physics concepts challenges your imagination and thinking potential, wherein, if you visualize a problem, then you can come up with a solution. So here is the promised list which will help you out.
Mechanics
Motion in One Dimension
The formulas for motion in one dimension (Also called Kinematical equations of motion) are as follows. (Here ‘u’ is initial velocity, ‘v’ is final velocity, ‘a’ is acceleration and t is time):
- s = ut + ½ at2
- v = u + at
- v2 = u2 + 2as
- vav (Average Velocity) = (v+u)/2
Momentum, Force and Impulse
Formulas for momentum, impulse and force concerning a particle moving in 3 dimensions are as follows (Here force, momentum and velocity are vectors ):
- Momentum is the product of mass and velocity of a body. Momentum is calculate using the formula: P = m (mass) x v (velocity)
- Force can defined as something which causes a change in momentum of a body. Force is given by the celebrated newton’s law of motion: F = m (mass) x a (acceleration)
- Impulse is a large force applied in a very short time period. The strike of a hammer is an impulse. Impulse is given by I = m(v-u)
Pressure
| Pressure (P) = | Force (F)
Area (A) |
Density
Density is the mass contained in a body per unit volume.
The formula for density is:
| Density (D) = | Mass(M)
Volume (V) |
Angular Momentum
Angular momentum is an analogous quantity to linear momentum in which the body is undergoing rotational motion. The formula for angular momentum (J) is given by:
J = r x p
where J denotes angular momentum, r is radius vector and p is linear momentum.
Torque
Circular Motion
The formulas for circular motion of an object of mass ‘m’ moving in a circle of radius ‘r’ at a tangential velocity ‘v’ are as follows:
| Centripetal force (F) = | mv2
r |
| Centripetal Acceleration (a) = | v2
r |
Center of Mass
| R = | ΣNi = 1 miri
ΣNi = 1mi |
where R is the position vector for center of mass, r is the generic position vector for all the particles of the object and N is the total number of particles.
Reduced Mass for two Interacting Bodies
The physics formula for reduced mass (μ) is :
| μ = | m1m2
m1 + m2 |
where m1 is mass of the first body, m2 is the mass of the second body.
Work and Energy
Formulas for work and energy in case of one dimensional motion are as follows:
W (Work Done) = F (Force) x D (Displacement)
Energy can be broadly classified into two types, Potential Energy and Kinetic Energy. In case of gravitational force, the potential energy is given by
P.E.(Gravitational) = m (Mass) x g (Acceleration due to Gravity) x h (Height)
The transitional kinetic energy is given by ½ m (mass) x v2(velocity squared)
Power
| Power (P) = | V2
R |
=I2R |
where P=power, W = Work, t = time.
Friction
Static friction is characterized by a coefficient of static friction μ . Coefficient of static friction is defined as the ratio of applied tangential force (F) which can induce sliding, to the normal force between surfaces in contact with each other. The formula to calculate this static coefficient is as follows:
| μ = | Applied Tangential Force (F)
Normal Force(N) |
The amount of force required to slide a solid resting on flat surface depends on the co efficient of static friction and is given by the formula:
FHorizontal = μ x M(Mass of solid) x g (acceleration)
Dynamic Friction:
Dynamic friction is also characterized by the same coefficient of friction as static friction and therefore formula for calculating coefficient of dynamic friction is also the same as above. Only the dynamic friction coefficient is generally lower than the static one as the applied force required to overcome normal force is lesser.
Moment of Inertia
| Object | Axis | Moment of Inertia |
| Disk | Axis parallel to disc, passing through the center | MR2/2 |
| Disk | Axis passing through the center and perpendicular to disc | MR2/2 |
| Thin Rod | Axis perpendicular to the Rod and passing through center | ML2/12 |
| Solid Sphere | Axis passing through the center | 2MR2/5 |
| Solid Shell | Axis passing through the center | 2MR2/3 |
Newtonian Gravity
| Fg = | Gm1m2
r2 |
where
- m1, m2 are the masses of two bodies
- G is the universal gravitational constant which has a value of 6.67300 × 10-11 m3 kg-1 s-2
- r is distance between the two bodies
Formula for escape velocity (vesc) = (2GM / R)1/2where,
- M is mass of central gravitating body
- R is radius of the central body
Projectile Motion
| Maximum height of projectile (h) = | v0 2sin2θ
2g |
Horizontal range of projectile (l) = v0 2sin 2θ / g
- l is the length of the pendulum
- g is acceleration due to gravity
Conical Pendulum
The Period of a conical pendulum (T) = 2π √(lcosθ/g)
where
- l is the length of the pendulum
- g is acceleration due to gravity
- Half angle of the conical pendulum
Electricity
Ohm’s Law
Ohm’s law gives a relation between the voltage applied a current flowing across a solid conductor:
V (Voltage) = I (Current) x R (Resistance)
Power
In case of a closed electrical circuit with applied voltage V and resistance R, through which current I is flowing,
| Power (P) = | V2
R |
= I2R. . . (because V = IR, Ohm’s Law)
Kirchoff’s Voltage Law
For every loop in an electrical circuit:
ΣiVi = 0
where Vi are all the voltages applied across the circuit.
Kirchoff’s Current Law
At every node of an electrical circuit:
ΣiIi = 0
where Ii are all the currents flowing towards or away from the node in the circuit.
Resistance
The physics formulas for equivalent resistance in case of parallel and series combination are as follows:
Resistances R1, R2, R3 in series:
Req = R1 + R2 + R3
Resistances R1 and R2 in parallel:
| Req = | R1R2
R1 + R2 |
For n number of resistors, R1, R2…Rn, the formula will be:
1/Req = 1/R1 + 1/R2 + 1/R3…+ 1/Rn
Capacitors
A capacitor stores electrical energy, when placed in an electric field. A typical capacitor consists of two conductors separated by a dielectric or insulating material. Here are the most important formulas related to capacitors. Unit of capacitance is Farad (F) and its values are generally specified in mF (micro Farad = 10 -6 F).
Capacitance (C) = Q / V
Energy Stored in a Capacitor (Ecap) = 1/2 CV2= 1/2 (Q2 / C) = 1/2 (QV)
Current Flowing Through a Capacitor I = C (dV / dt)
Equivalent capacitance for ‘n’ capacitors connected in parallel:
Ceq (Parallel) = C1 + C2 + C3…+ Cn = Σi=1 to n Ci
Equivalent capacitance for ‘n’ capacitors in series:
1 / Ceq (Series) = 1 / C1 + 1 / C2…+ 1 / Cn = Σi=1 to n (1 / Ci)
Here
- C is the capacitance
- Q is the charge stored on each conductor in the capacitor
- V is the potential difference across the capacitor
Parallel Plate Capacitor Formula:
C = kε0 (A/d)
Where
- k = dielectric constant (k = 1 in vacuum)
- ε0 = Permittivity of Free Space (= 8.85 × 10-12 C2 / Nm2)
- A = Plate Area (in square meters)
- d = Plate Separation (in meters)
Cylinrical Capacitor Formula:
C = 2π kε0 [L / ln(b / a)]
Where
- k = dielectric constant (k = 1 in vacuum)
- ε0 = Permittivity of Free Space (= 8.85 × 10-12 C2 / Nm2)
- L = Capacitor Length
- a = Inner conductor radius
- b = Outer conductor radius
Spherical Capacitor Formula:
C = 4π kε0 [(ab)/(b-a)]
Where
- k = dielectric constant (k = 1 in vacuum)
- ε0 = Permittivity of Free Space (= 8.85 × 10-12 C2 / Nm2)
- a = Inner conductor radius
- b = Outer conductor radius
Inductors
An inductor is an electrical component which resists the flow of electrons or electric current through it. This property of inductance, in these devices, is caused by the electromotive force, created by magnetic field induced in them. The unit of inductance is Henry. Here are some important formulas associated with inductors.
Energy Stored in Inductor (Estored) = 1/2 (LI2)
Where, L is inductance and I is the current flowing through the inductor.
Inductance of a cylindrical air core Coil (L) = (m0KN2A / l)
Where
- L is inductance measured in Henries
- N is the number of turns on the coil
- A is cross-sectional area of the coil
- m0 is the permeability of free space (= 4π × 10-7 H/m)
- K is the Nagaoka coefficient
- l is the length of coil
Inductors in a Series Network
For inductors, L1, L2…Ln connected in series,
Leq = L1 + L2…+ Ln (L is inductance)
Inductors in a Parallel Network
For inductors, L1, L2…Ln connected in parallel,
1 / Leq = 1 / L1 + 1 / L2…+ 1 / Ln
Thermodynamics Formulas
Thermodynamics is a vast field providing an analysis of the behavior of matter in bulk. It’s a field focused on studying matter and energy in all their manifestations. Here are some of the most important formulas associated with classical thermodynamics and statistical physics.
First Law of Thermodynamics
dU = dQ + dW
where, dU is the change in internal energy, dQ is the heat absorbed by the system and dW is the work done on the system.
Thermodynamic Potentials
All of thermodynamical phenomena can be understood in terms of the changes in five thermodynamic potentials under various physical constraints. They are Internal Energy (U), Enthalpy (H), Helmholtz Free Energy (F), Gibbs Free Energy (G), Landau or Grand Potential (Φ). Each of these scalar quantities represents the potentiality of a thermodynamic system to do work of various kinds under different types of constraints on its physical parameters.
| Thermodynamic Potential | Defining Equation |
|
| Internal Energy (U) | dU = TdS − pdV + µdN | |
| Enthalpy (H) | H = U + pV dH = TdS + Vdp + µdN |
|
| Gibbs Free Energy (G) | G = U – TS + pV = F + pV = H – TS dG = -SdT + Vdp + µdN |
|
| Helmholtz Free Energy (F) | F = U – TS dF = – SdT – pdV + µdN |
|
| Landau or Grand Potential | Φ = F – µN dΦ = – SdT – pdV – Ndµ |
Ideal Gas Equations
An ideal gas is a physicist’s conception of a perfect gas composed of non-interacting particles which are easier to analyze, compared to real gases, which are much more complex, consisting of interacting particles. The resulting equations and laws of an ideal gas conform with the nature of real gases under certain conditions, though they fail to make exact predictions due the interactivity of molecules, which is not taken into consideration. Here are some of the most important physics formulas and equations, associated with ideal gases. Let’s begin with the prime ideal gas laws and the equation of state of an ideal gas.
| Law | Equation |
|
| Boyle’s Law | PV = Constant or P1V1 = P2V2 (At Constant Temperature) |
|
| Charles’s Law | V / T = Constant or V1 / T1 = V2 / T2 (At Constant Pressure) |
|
| Amontons’ Law of Pressure-Temperature | P / T = Constant or P1 / T1 = P2 / T2 (At Constant Volume) |
|
| Equation of State For An Ideal Gas | PV = nRT = NkT |
Kinetic Theory of Gases
Based on the primary assumptions that the volume of atoms or molecules is negligible, compared to the container volume and the attractive forces between molecules are negligible, the kinetic theory describes the properties of ideal gases. Here are the most important physics formulas related to the kinetic theory of monatomic gases.
Pressure (P) = 1/3 (Nm v2)
Here, P is pressure, N is the number of molecules and v2 is the mean squared particle velocity.
Internal Energy (U) = 3/2 (NkT)
Heat Capacities
Heat Capacity at Constant Pressure (Cp) = 5/2 Nk = Cv + Nk
Heat Capacity at Constant Volume (Cv) = 3/2 Nk
Ratio of Heat Capacities (γ) = Cp / Cv = 5/3
Velocity Formulas
Root Mean Square Velocity of a Molecule (Vrms) = (3kT/m)1/2
Most Probable Velocity of a Molecule (Vprob) = (2kT/m)1/2
Mean Free Path of a Molecule (λ) = (kT)/√2πd2P (Here P is in Pascals)
Here N is the number of molecules, k is the Boltzmann constant, P is pressure, d is the molecular diameter, m is mass of the molecule and T is the gas temperature.
Electromagnetism
| (F) = | q1q2
4πε0r2 |
Here,
- q1, q2 are charges
- ε0 is the permittivity of free space
- r is the distance between the two charges
Lorentz Force
The Lorentz force is the force exerted by an electric and/or magnetic field on a charged particle.
(Lorentz Force) F = q (E + v x B)
where
- q is the charge on the particle
- E and B are the electric and magnetic field vectors
Relativistic Mechanics
Here are some of the most important relativistic mechanics formulas. The transition from classical to relativistic mechanics is not at all smooth, as it merges space and time into one by taking away the Newtonian idea of absolute time. If you know what is Einstein’s special theory of relativity, then the following formulas will make sense to you.
Lorentz Transformations
Lorentz transformations can be perceived as rotations in four dimensional space. Just as rotations in 3D space mixes the space coordinates, a Lorentz transformation mixes time and space coordinates. Consider two, three dimensional frames of reference S(x,y,z) and S'(x’,y’,z’) coinciding with each other.
Now consider that frame S’ starts moving with a constant velocity v with respect to S frame. In relativistic mechanics, time is relative! So the time coordinate for the S’ frame will be t’ while that for S frame will be t.
Consider
| γ = | 1
√(1 – v2/c2) |
The coordinate transformations between the two frames are known as Lorentz transformations and are given as follows:
Lorentz Transformations of Space and Time
x = γ (x’ + vt’) and x’ = γ (x – vt)
y = y’
z= z’
t = γ(t’ + vx’/c2) and t’ = γ(t – vx/c2)
Relativistic Velocity Transformations
In the same two frames S and S’, the transformations for velocity components will be as follows (Here (Ux, Uy, Uz) and (Ux‘, Uy‘, Uz‘) are the velocity components in S and S’ frames respectively):
Ux = (Ux‘ + v) / (1 + Ux‘v / c2)
Uy = (Uy‘) / γ(1 + Ux‘v / c2)
Uz = (Uz‘) / γ(1 + Ux‘v / c2) and
Ux‘ = (Ux – v) / (1 – Uxv / c2)
Uy‘ = (Uy) / γ(1 – Uxv / c2)
Uz‘ = (Uz) / γ(1 – Uxv / c2)
Momentum and Energy Transformations in Relativistic Mechanics
Consider the same two frames (S, S’) as in case of Lorentz coordinate transformations above. S’ is moving at a velocity ‘v’ along the x-axis. Here again γis the Lorentz factor. In S frame (Px, Py, Pz) and in S’ frame (Px‘, Py‘, Pz‘) are momentum components. Now we consider formulas for momentum and energy transformations for a particle, between these two reference frames in relativistic regime.
Component wise Momentum Transformations and Energy Transformations
Px = γ(Px‘ + vE’ / c2)
Py = Py‘
Pz = Pz‘
E = γ(E’ + vPx)
and
Px‘ = γ(Px – vE’ / c2)
Py‘ = Py
Pz‘ = Pz
E’ = γ(E – vPx)
Physical Formulas for Quantities in Relativistic Dynamics
All the known quantities in classical mechanics get modified, when we switch over to relativistic mechanics which is based on the special theory of relativity. Here are formulas of quantities in relativistic dynamics.
Relativistic momentum p = γm0v
where m0 is the rest mass of the particle.
Rest mass energy E = m0c2
Total Energy (Relativistic) E = √(p2c2 + m02c4))
Optics
Snell’s Law
| Sin i
Sin r |
= | n2
n1 |
= | v1
v2 |
- where i is angle of incidence
- r is the angle of refraction
- n1 is refractive index of medium 1
- n2 is refractive index of medium 2
- v1, v2 are the velocities of light in medium 1 and medium 2 respectively
Gauss Lens Formula: 1/u + 1/v = 1/f
where
- u – object distance
- v – image distance
- f – Focal length of the lens
Lens Maker’s Equation
The most fundamental property of any optical lens is its ability to converge or diverge rays of light, which is measued by its focal length. Here is the lens maker’s formula, which can help you calculate the focal length of a lens, from its physical parameters.
1 / f = [n-1][(1 / R1) – (1 / R2) + (n-1) d / nR1R2)]
Here,
- n is refractive index of the lens material
- R1 is the radius of curvature of the lens surface, facing the light source
- R2 is the radius of curvature of the lens surface, facing away from the light source
- d is the lens thickness
If the lens is very thin, compared to the distances – R1 and R2, the above formula can be approximated to:
(Thin Lens Approximation) 1 / f ≈ (n-1) [1 / R1– 1 / R2]
Compound Lenses
The combined focal length (f) of two thin lenses, with focal length f1 and f2, in contact with each other:
1 / f = 1 / f1 + 1 / f2
If the two thin lenses are separated by distance d, their combined focal length is provided by the formula:
1 / f = 1 / f1 + 1 / f2 – (d / f1 – f2))
Newton’s Rings Formulas
Here are the important formulas for Newton’s rings experiment which illustrates diffraction.
nth Dark ring formula: r2n = nRλ
nth Bright ring formula: r2n = (n + ½) Rλ
where
- nth ring radius
- Radius of curvature of the lens
- Wavelength of incident light wave
Quantum Physics
De Broglie Wave
| λ = | h
p |
where, λ- De Broglie Wavelength, h – Planck’s Constant, p is momentum of the particle.
Bragg’s Law of Diffraction: 2a Sin θ = nλ
where
- a – Distance between atomic planes
- n – Order of Diffraction
- θ – Angle of Diffraction
- λ – Wavelength of incident radiation
Planck Relation
| E = hv = | hω
2π |
where h is Planck’s Constant, v the frequency of radiation and ω = 2πv
Uncertainty Principle
Position-Momentum Uncertainty
What the position-momentum uncertainty relation says is, you cannot predict where a particle is and how fast it is moving, both, with arbitrary accuracy. The more precise you are about the position, more uncertain will you be about the particle’s momentum and vice versa. The mathematical statement of this relation is given as follows:
| Δx.Δp ≥ | h
2π |
where Δx is the uncertainty in position and Δp is the uncertainty in momentum.
Energy-Time Uncertainty
This is an uncertainty relation between energy and time. This relation gives rise to some astounding results like, creation of virtual particles for arbitrarily short periods of time! It is mathematically stated as follows:
| ΔE.Δt ≥ | h
2π |
where ΔE is the uncertainty in energy and Δt is the uncertainty in time.
This concludes my review of some of the important physics formulas. This list, is only representative and is by no means anywhere near complete. Physics is the basis of all sciences and therefore its domain extends over all sciences. Every branch of physics theory abounds with countless formulas. If you resort to just mugging up all these formulas, you may pass exams, but you will not be doing real physics. If you grasp the underlying theory behind these formulas, physics will be simplified. To view physics through the formulas and laws, you must be good at maths. There is no way you can run away from it. Mathematics is the language of nature!
The more things we find out about nature, more words we need to describe them. This has led to increasing jargonization of science with fields and sub-fields getting generated. You could refer to a glossary of science terms and scientific definitions for any jargon that is beyond your comprehension.
If you really want to get a hang of what it means to be a physicist and get an insight into physicist’s view of things, read ‘Feynman Lectures on Physics’, which is highly recommended reading, for anyone who loves physics. It is written by one of the greatest physicists ever, Prof. Richard Feynman. Read and learn from the master. Solve as many problems as you can, on your own, to get a firm grasp of the subject.